What is the difference between linear chains and rings composed of the same material? The molecular building blocks are identical, but from a mathematical point of view the two structures have distinct topologies, namely ring and linear chain. This difference is readily recognizable on a macroscopic scale, as for example a golden ring and a gold bar, but represents a tricky task on the microscopic scale. The physicists Lisa Weiss and Christos Likos of the University of Vienna and Arash Nikoubashman of the Johannes-Gutenberg University of Mainz investigated strategies to separate nano- and microparticles of distinct topology. Their results are published in the high-impact journal ACS Macro Letters.
The purely mathematical property – linear or circular – can have severe consequences in the world of materials. Since circular molecules lack any ends, which could serve as a starting point for degradation, they are more resistant and less entangled. Nature profits from this unique property of circular molecules to increase DNA’s and RNA’s resilience against degradation. Topology plays not only a role in biology but as well when molecules get out of equilibrium: Linear and ring molecules flow differently, as do their mixtures.
This difference in flow can be explained using spaghetti as an analogy for linear molecules and stirring a pot of them as analogy for flow: Single noodles elongate in flow direction, although they are still entangled. Imagine, we now stir ring-shaped pasta corresponding to spaghetti with ends glued together: Circular pasta orients more easily in flow direction compared to linear Spaghetti and rings are less entangled, making stirring easier. Nevertheless, separating a mixture of linear and ring-shaped pasta in one pot into two separated systems of high purity is a challenging task, since the molecular building blocks are exactly the same. Both noodle topologies are made of the same dough. Tediously, we have to hand-pick one by one to distinguish if it is a spaghetto or a ring-shaped noodle. Such a process is impossible on a microscopic scale, hence the development of new materials based on different topologies is hindered, as well as the analysis of topology in biological systems. Therefore, we need new and efficient separation technologies.
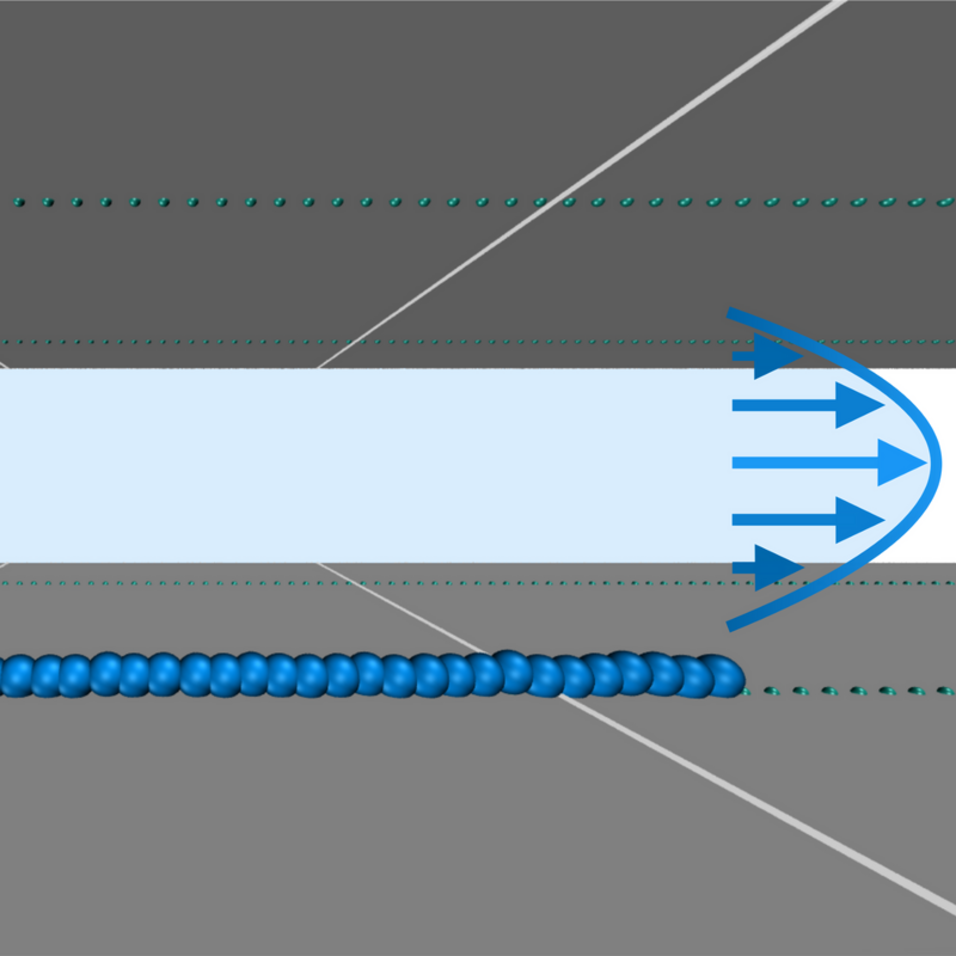
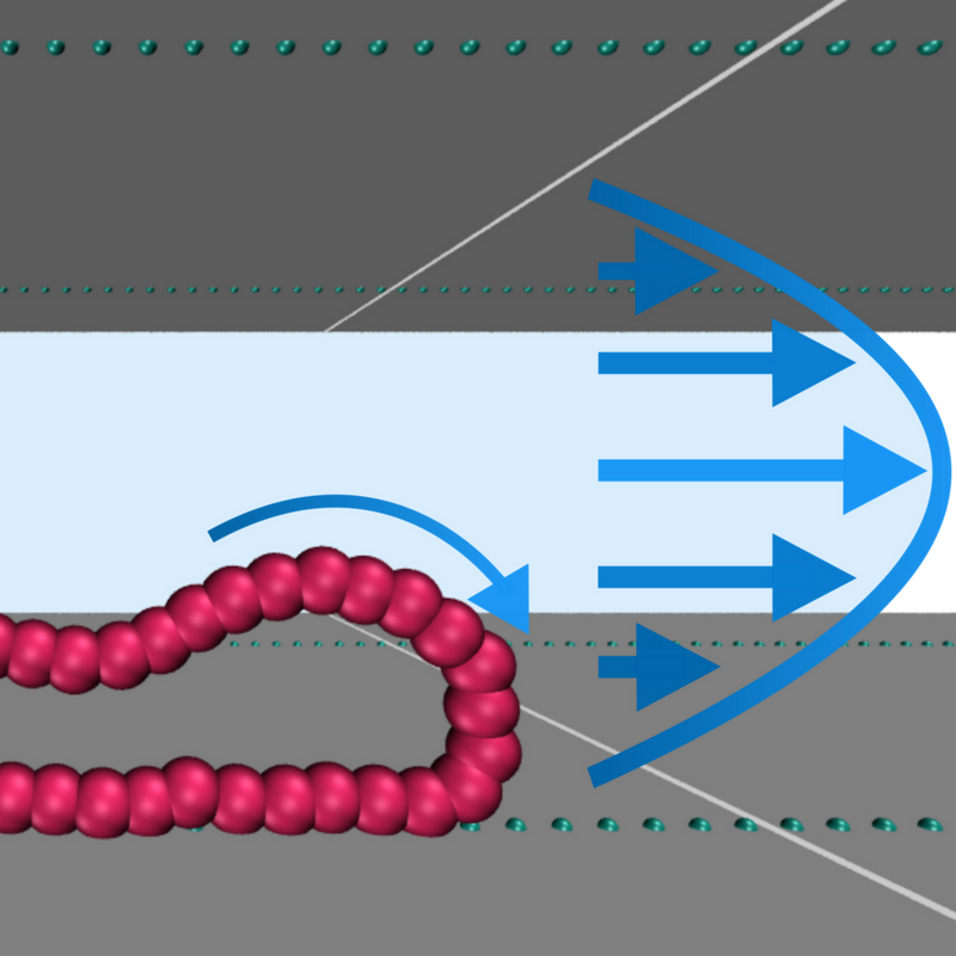
Researchers of the University of Vienna and the Johannes-Gutenberg-University of Mainz developed an automatized strategy to separate reliably circular molecules from their linear counterparts. Using computer simulations, they prove the effectiveness of microfluidic channels decorated with attractive spots. Those spots attract equally strongly the molecular building blocks of linear and ring molecules. Lisa Weiss of the Computational Physics Group at the University of Vienna explains that linear chains are immobilized on these spots, whereas ring molecules can roll along them, this rolling motion being possible only for topologies with a closed contour line. To purify the filter of the stuck chains, the channel is flushed with a non-solvent for the chains, i.e., a solvent in which the molecules cannot dissolve – as for example oil in water. Therefore, chains crumble and detach and, subsequently, the flow carries off the chains and the filter is clean.
The project has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement NO 674979-Nanotrans.
Publication in ACS Macro Letters:
Lisa B. Weiss, Arash Nikoubashman and Christos N. Likos: Topology-Sensitive Microfluidic Filter for Polymers of Varying Stiffness. In Macro Letters (2017)
http://dx.doi.org/10.1021/acsmacrolett.7b00768
Click here to read the original article.